This workbook evaluates the analytical solution for steady-state conduction in a unit square.  One boundary is held at a different temperature than the other three.  The output is a raised contour plot of the results.  Textbooks use this particular problem frequently to demonstrate separation-of-variables as a solution technique for PDE‘s. The user can change the number of terms to be included in the evaluation of the infinite series. A second worksheet (See below) animates the process of adding terms to the series. Quite a few are needed in this particular problem to get a good solution here – because of the discontinuities at two of the corners.   This animation shows the Gibbs phenomenon clearly.

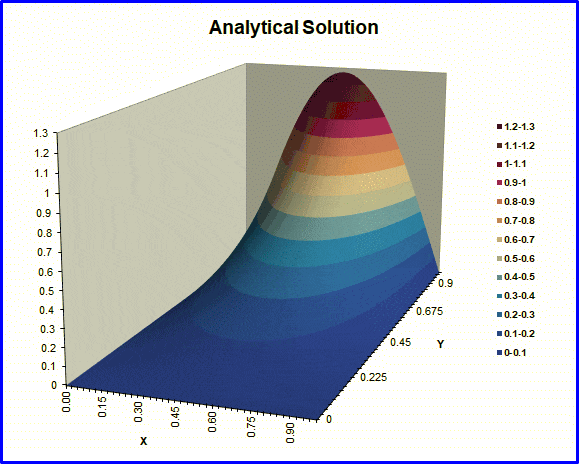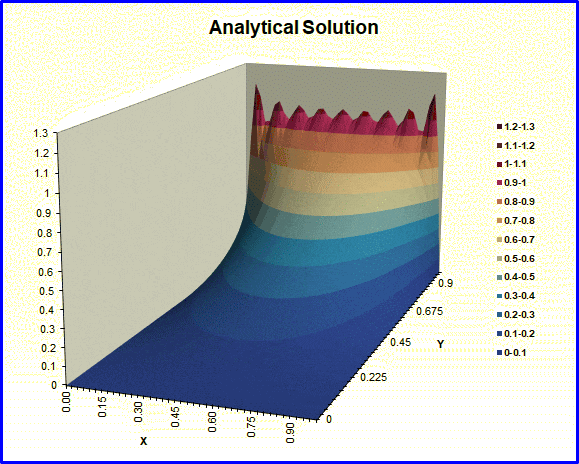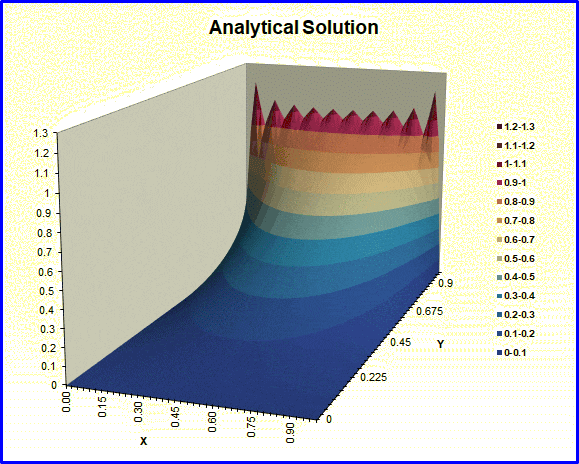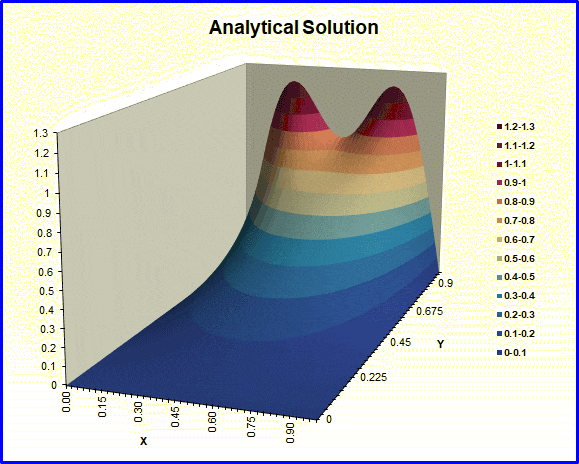
This workbook is by its very nature limited to one particular set of boundary conditions.   Our Visual Studio executable, HTT_2DSS, is applicable to a much wider set of conditions.   A numerical (finite-volume) solution for these same boundary conditions is included as an example in that executable.