Heat Transfer
For those looking for an entire software-enhanced introductory course in heat transfer, this table of contents is provided. The chapter numbering is typical of several popular textbooks in the field.
1. Introduction to Heat Transfer
2. Conduction Fundamentals
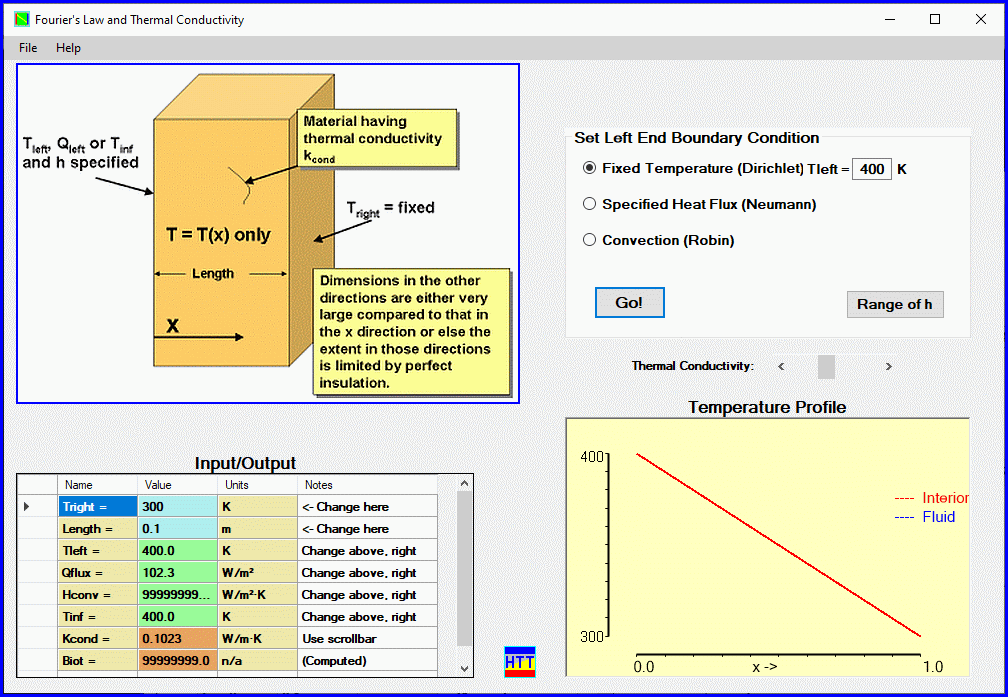
HTTFouriers.exe – Visual Studio module covering thermal conductivity and three types of thermal boundary conditions.
Airwater.xlsm – VBA Functions for properties of air and water as a function of temperature.
3. One-Dimensional, Steady-state Conduction
HTTextnd.exe – Visual Studio module for extended surface heat transfer (fins).
HTTtridiag.xlsm – 1-D, S-S conduction with generation in a plane wall. Evaluates analytical solution as well as a finite-volume solution with linear equations solved (1) directly using Thomas algorithm and, (2) by iteration.
HTTnetwork.xlsm – Includes series and parallel lumped models for 1-D conduction.
HTTHeatedInsulation.xlsm – 1-D, steady-state heat-generating, insulated cylinder.
HTTFuelPin.xlsm – Simple model of temperature distribution in a nuclear fuel pin.
HTTBesselFunctions.xlsm – Analytical solution for efficiency of a straight, annular fin.
Project: George Washington’s Compost Heap
Extra: Extended Surface (Fin) Heat Transfer Photos
4. Two-Dimensional, Steady-state Conduction
HTT_2dss.exe (Visual Studio module for 2-D, Steady-state Conduction)
Exercises – Workbook set up to record results from HTT_2dss module.
HTTtwodss.xlsm (Excel workbook demonstrating the evaluation and display of an analytical solution built up term-by-term for one particular 2-D, SS problem)
HTTiterdemos.xlsm (Excel workbook demonstrating iteration as a means of solving linear equations)
HTTConductionShapeFactors.xlsm (Excel workbook compilation of shape factors)
LinearEquations.xlsm (Excel workbook demonstrating both use of Excel’s supplied functions for solving linear equations and of a VBA subprogram for matrix inversion).
5. Transient Conduction
HTTonedt.exe (Visual Studio module for 1-D, Transient Conduction (Burn your Heisler Charts!))
HTT_Cook.exe (Visual Studio module for Transient Conduction in a Finite-length Cylinder
HTTtransanal.xlsm (Excel workbook evaluating analytical (separation of variables) solution for transient conduction in plane wall)
HTTsemicalc.xlsm (Excel workbook for periodic conduction in a semi-infinite body)
Project: Monticello Transient Conduction Problem with a time-dependent convective boundary condition
Student Project: Transient Conduction at the Interface between Two Materials
Project: Sandwich Wall (ICF) Construction
Extra: ICFHouse.pptx
Extra: Ground Source Heat Pump
6. Fundamentals of Convection
Extra: Penguins.mp4 – Thermal Design and Family Life Issues in Emperor Penguins
7. External Forced Flow
HTTblasius.xlsm – Laminar flow over a heated flat plate using similarity method
HTTflatp.exe – Visual Studio virtual laboratory for laminar and turbulent flow over a flat plate
HTTBLCalcs.xlsm – Evaluate standard correlations for mixed convection over a flat plate and for a flat plate with unheated starting length
HTTtubeBanksZukauskas.xlsm – Empirical correlations for inline and staggered tube bundles.
Project: Convective Heat and Mass Transfer from a Runner
Project: Evaporative Cooling of Water in a Lister (Lyster) Bag.
Student Project: Self-similar Boundary Layer Calculations
8. Internal Flows
HTT_pipe.exe – Visual Studio virtual laboratory for laminar and turbulent, thermal-entry-length flow
Corr_int.xlsm – Implementation of common correlations for internal flow forced convection.
HTTRoughPipes.xlsm – Convection coefficients for rough pipes using the Colebrook equation for fluid mechanics with the Gnielinski correlation for heat transfer.
9. Natural Convection Flows
HTTncvfp.exe – Visual Studio virtual laboratory for natural convection adjacent to a vertical, flat plate calculated using classical similarity methods.
HTTporus.exe – Visual Studio virtual laboratory for natural convection in a saturated, permeable layer
10. Heat Transfer with Phase Change (Boiling and Condensation)
Extra: Trans-Alaska Pipeline Passive Cooling System
11. Heat Exchangers
HTT_HX.exe – Visual Studio executable for design and performance calculations of “1-D” heat exchangers, i.e., simple parallel and counter-flow, shell-and-tube and parallel plate (first tab). Design and performance calculations of “2-D” heat exchangers, i.e., cross-flow HX’s are on the 2nd tab.
HxEffectivenssNTU.xlsm – Effectiveness-NTU relations for a variety of HX geometries in algebraic, tabular, graphical and user-function forms.
Extra: Heat Exchanger Photos
12. Radiation Fundamentals
HTTplnkslaw.xlsm – Calculation of blackbody emission spectrum and the blackbody integral as a function of temperature.
Project: Transmissivity of Glass
13. Radiative Exchange
HTTviewfactor.xlsm – This Excel workbook computes the view factors for four geometries for which analytical solutions are available and for which graphs are usually provided in textbooks. Both display the input geometry to scale on the screen so that the user can check it carefully. It also computes the view factor for rectangles in parallel planes and for rectangles in perpendicular planes. Another worksheet calculates the view factor between two arbitrarily-oriented parallelograms using a computer implementation of the Nusselt Unit-Sphere Method.
HTTnetwork.xlsm – In addition to several examples using a DC network analogy for steady-state conduction, this spreadsheet includes several examples using the DC network analogy for gray body radiation.
HTTradiosity.xlsm – This Excel workbook provides a template for solving radiative exchange problems involving as many as 20 diffuse-gray surfaces exchanging heat among themselves.
Thermodynamics
Thermodynamic Properties
ProperT.xlsm – Properties of Fluids Using the free CoolProp Excel Add-in
MollierDiagram.xlsm – Mollier (Enthalpy-Entropy) Diagram
Extensive and Intensive Properties
Thermodynamic Processes
Thermodynamic Cycles
Power Cycles
Otto (Spark Ignition) Cycle Template
Diesel (Compression Ignition) Cycle Template
Brayton (Jet Engine) Cycle Template
Ocean Thermal Energy Conversion (Rankine Cycle)
Refrigeration and Heat Pump Cycles
Vapor Compression Refrigeration Cycle
Residential Heat Pump in Winter
Extra: Ground Source Heat Pump
Fluid Mechanics
Aerodynamics
Wingtip Vortex Motion above a Runway
Vortex Panel Method for a 2D Lifting Airfoil
Real Fluids
Solution of Blasius Equation by Shooting
Compressible Flows
1D Compressible Flows (Isentropic flow with area change, normal shocks, Fanno line, Rayleigh line)
Computational Fluid Dynamics
Advection of a Passive Scalar in One and Two Dimensions
Elliptic Grid Generation for odd geometries
Applications
Velocity Triangles for Turbomachinery
Projectile Motion with Air Resistance Using 4th order Runge-Kutta