This workbook performs a numerical solution of the Blasius equation for flow in a laminar, self-similar, flat plate boundary layer. It uses a Runge-Kutta integration scheme and a shooting algorithm used to solve this third-order, non-linear, ordinary differential equation. This algorithm is from An Introduction to Computational Fluid Mechanics by C.Y. Chow and is embellished with Excel graphics. Once the value of f'(∞) is close to the desired value (1.0), we use a half-interval method to correct f”(0) until the converged value is found. We provide tabulated results from a classical source (Howarth’s results as reported in Schlicting) for comparison with the current solution.
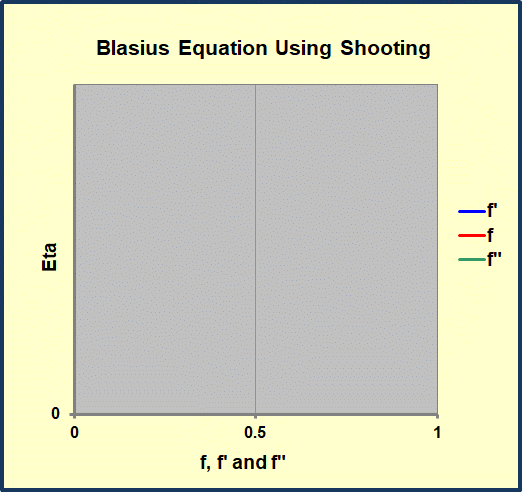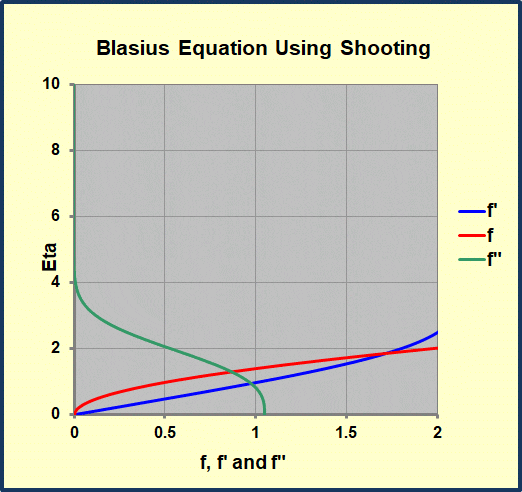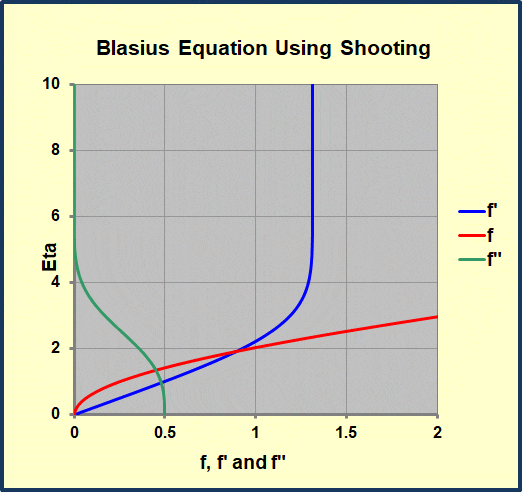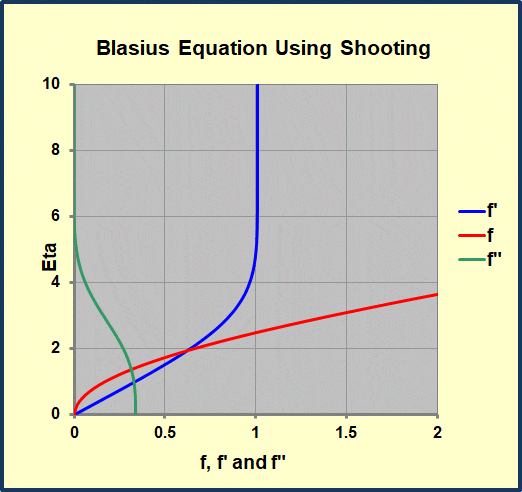
The “.332” appearing in the correlation for laminar, forced convection on a flat plate follows directly from the value of f”(0) found eventually in the above calculation.
